要介绍这两个概念，需要先介绍一个简单的概念；中值（median）。

中值简单的说，就是一堆给定的数字，最中间的值；

例如：1，2，3，4，5的中值就是3；

1，2，3，4的中值就是2.5；

引入数学公式就是：

If _n_ is odd then Median ( _M_ ) = value of (( _n_ + 1)/2)th item term.

If _n_ is even then Median ( _M_ ) = value of [(( _n_ )/2)th item term +
(( _n_ )/2 + 1)th item term ]/2

http://en.wikipedia.org/wiki/Median

什么是quartile呢？quartile的意思是四分位数，second quartile就是中值；

四分位数，从字面上看是四个数字将一堆数分割开来，对，就是分割；

第一个四分位数(Q1)，也叫做25th percentile或者lower quartile；

第二个四分位数(Q2)，也叫做中值或者50th percentile；

第三个四分位数(Q3)，也叫做75th percentile或者upper quartile；

interquartile range(IQR)，IQR=Q3-Q1;

四分位数的计算方法有很多，下面是从wikipedia复制过来的。

Method 1

1. Use the median to divide the ordered data set into two halves. Do not include the median in either half.使用中值将有序的数据集分成两部分，这两部分不包括中值

2. The lower quartile value is the median of the lower half of the data. The upper quartile value is the median of the upper half of the data.Q1就是小数据部分的中值，Q3就是大数据的中值

Method 2

1. Use the median to divide the ordered data set into two halves. If the median is a datum (as opposed to being the mean of the middle two data), include the median in both halves.使用中值将有序的数据集分成两部分，数据集的个数的奇数的话，将中值加入到分成的两部分的末尾和头
2. The lower quartile value is the median of the lower half of the data. The upper quartile value is the median of the upper half of the data.和方法1一样

Method 3

1. If there are an even number of data points, then the method is the same as above.如果数据集是偶数的话，同上；

2. If there are (4 _n_ +1) data points, then the lower quartile is 25% of the _n_ th data value plus 75% of the ( _n_ +1)th data value; the upper quartile is 75% of the (3 _n_ +1)th data point plus 25% of the (3 _n_ +2)th data point.如果数据集是4n+1个的话，Q1=Set[n]25%+Set[n+1]75%;Q3=Set[3n+1]75%+Set[3n+2]25%

3. If there are (4 _n_ +3) data points, then the lower quartile is 75% of the ( _n_ +1)th data value plus 25% of the ( _n_ +2)th data value; the upper quartile is 25% of the (3 _n_ +2)th data point plus 75% of the (3 _n_ +3)th data point.如果数据集是4n+3个的话，Q1=Set[n+1]75%+Set[n+2]25%; Q3=Set[3n+2]25%+Set[3n+3]75%

Example 1

Ordered Data Set: 6, 7, 15, 36, 39, 40, 41, 42, 43, 47, 49

Method 1	Method 2	Method 3

|
|

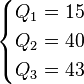
Example 2

Ordered Data Set: 7, 15, 36, 39, 40, 41

As there are an even number of data points, all three methods give the same
results.

Method 1	Method 2	Method 3

|
|

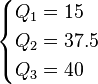
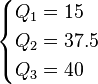
需要一提的是，如果数据比Q1-1.5IQR小，比Q3+1.5IQR大的话，我们称之为outiler（异常值）

http://en.wikipedia.org/wiki/Quartile

什么是percentile呢？percentile的意思是百分位数，50th percentile就是中值；25th percentile就是Q1；

percentile怎样计算呢？

例如：

First worked example of the Nearest Rank method

Consider the ordered list {15, 20, 35, 40, 50}, which contains five data
values. What are the 30th, 40th, 50th and 100th percentiles of this list using
the Nearest Rank method?

Percentile
P | Number in list
N | Ordinal rank
n | Number from the ordered list
that has that rank | Percentile
value | Notes
—|—|—|—|—|—
30th | 5 |
| the second number in the ordered list, which is 20 | 20 | 20 is an
element of the list
40th | 5 |
| the second number in the ordered list, which is 20 | 20 | In this
example it is the same as the 30th percentile.
50th | 5 |
| the third number in the ordered list, which is 35 | 35 | 35 is an
element of the ordered list.
100th | 5 | Last | 50, which is the last number in the ordered list |
50 | The 100th percentile is defined to be the largest value in the list,
which is 50.

http://en.wikipedia.org/wiki/Percentile